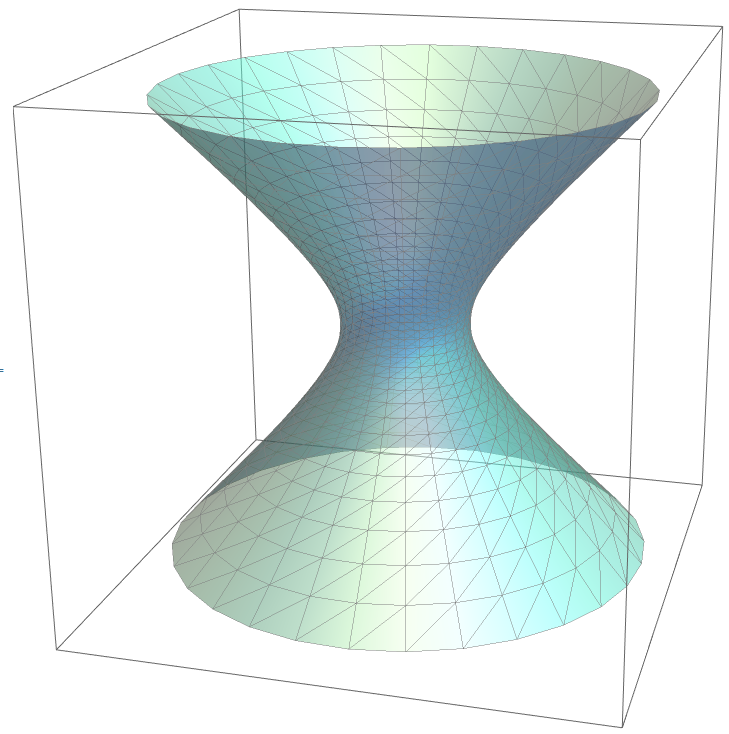
Hyperboloid Of One Sheet Formula

Hyperboloid Of One Sheet Formula - Web hyperboloid of one sheet: Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). You have to see it. Red or blue) hyperboloid of one sheet: Describe the traces of the hyperboloid of. X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. You can find the only remaining unknown c by plugging in its value into the the equation. The following parametric representation includes hyperboloids of. Generation by a rotating hyperbola (top) and line (bottom: Web the hyperboloid of one sheet.

For one thing, its equation is. X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. You have to see it. Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Web hyperboloid of one sheet: Web the hyperboloid of one sheet. The following parametric representation includes hyperboloids of. Red or blue) hyperboloid of one sheet: The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. You can find the only remaining unknown c by plugging in its value into the the equation.

Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Web the hyperboloid of one sheet. For one thing, its equation is. Web hyperboloid of one sheet: The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. Red or blue) hyperboloid of one sheet: X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. Describe the traces of the hyperboloid of. You can find the only remaining unknown c by plugging in its value into the the equation. Generation by a rotating hyperbola (top) and line (bottom:

Solution curves on the hyperboloid of onesheet Download Scientific

X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. The following parametric representation includes hyperboloids of. Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Red or blue) hyperboloid of one.

Quadratic Surfaces Hyperboloid of One Sheet Visions in Math

The following parametric representation includes hyperboloids of. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. Describe the traces of the hyperboloid of. Web hyperboloid of one sheet:

Quadric Surfaces Calculus III

Generation by a rotating hyperbola (top) and line (bottom: Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Web the hyperboloid of one sheet. The following parametric representation includes hyperboloids of. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces.

Special Hyperboloid of 1 Sheet as a Locus GeoGebra

You have to see it. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. Web hyperboloid of one sheet: Web a hyperboloid of one sheet is any surface.

Hyperboloid of One Sheet

Web the hyperboloid of one sheet. Describe the traces of the hyperboloid of. X2 a2 + y2 b2 − z2 c2 = 1 x 2 a 2 + y 2 b 2 − z 2 c 2 = 1. Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\)..

Hyperboloids

Red or blue) hyperboloid of one sheet: Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). The following parametric representation includes hyperboloids of. For one thing, its equation is. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces.

Hyperboloid of One Sheet

Web hyperboloid of one sheet: Describe the traces of the hyperboloid of. For one thing, its equation is. Web the hyperboloid of one sheet. You can find the only remaining unknown c by plugging in its value into the the equation.

Quadric Surfaces (Identified and Explained w/ Examples!)

For one thing, its equation is. Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). The following parametric representation includes hyperboloids of. Describe the traces of the hyperboloid of. Web the hyperboloid of one sheet.

Quadric Surface The Hyperboloid of Two Sheets YouTube

You have to see it. The following parametric representation includes hyperboloids of. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. Red or blue) hyperboloid of one sheet: For one thing, its equation is.

Hyperboloid of TWO Sheets

You have to see it. You can find the only remaining unknown c by plugging in its value into the the equation. Generation by a rotating hyperbola (top) and line (bottom: Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Describe the traces of the hyperboloid of.

Web Hyperboloid Of One Sheet:

The following parametric representation includes hyperboloids of. Red or blue) hyperboloid of one sheet: You have to see it. Web the hyperboloid of one sheet.

You Can Find The Only Remaining Unknown C By Plugging In Its Value Into The The Equation.

Web a hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Describe the traces of the hyperboloid of. For one thing, its equation is. The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces.